需要定制解决方案来应对最复杂的电磁挑战?

创新的电磁仿真软件和卓越的技术支持,可缩短设备投放市场的时间并降低成本。
30 年来一直是电磁仿真软件的领先供应商
多功能工具和敏捷结构
Remcom 为商业用户和美国政府赞助商提供创新的电磁仿真软件和无线传播软件。Remcom 的全套互补产品相互配合,为现实世界中的复杂设备提供完整的端到端设计和分析,简化了包括天线设计和布置在内的各种应用的电磁分析、
- 5G MIMO
- 室外和室内毫米波规划
- 移动设备设计
- 生物效应
- 微波设备分析
- 汽车雷达
...以及更多
Remcom 软件
Remcom 的产品可协同工作,提供完整准确的结果。
-
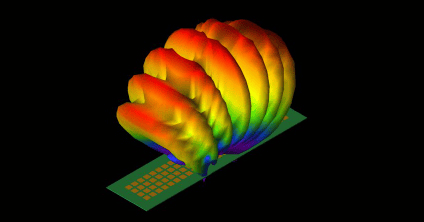
XFdtd® 三维电磁仿真软件
XFdtd 三维电磁仿真软件为工程师提供了强大的工具,帮助他们缩短开发时间,更快地将产品投放市场。 XFdtd 是一款功能全面的电磁仿真求解器,随着未知数数量的增加,它在效率方面超越了其他方法。
进一步了解 XFdtd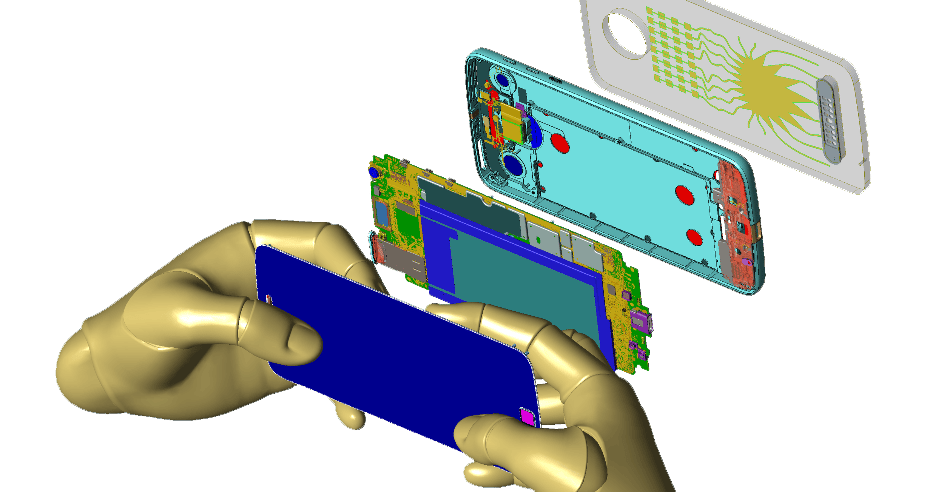
-
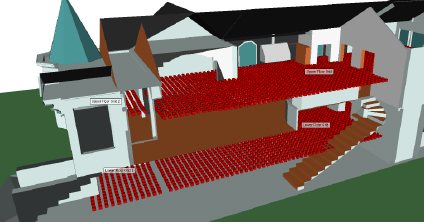
Wireless InSite® 3D 无线预测软件
Wireless InSite 是一套射频传播模型,提供三维射线跟踪、基于射线的快速方法和经验模型,用于分析特定场所的无线电波传播和无线通信系统。通过综合建模、模拟和后处理功能,它能高效、准确地预测复杂的城市、室内、农村和混合路径环境中的电磁波传播和通信信道特性。
进一步了解 Wireless InSite
-
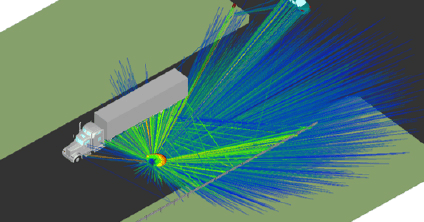
WaveFarer® 雷达模拟软件
WaveFarer 是一款高保真雷达模拟器,可计算雷达系统周围环境中结构和车辆的多径和散射,以及频率高达和超过 100 GHz 的主要大气和散射效应。其应用包括模拟汽车驾驶场景、室内传感器和远场雷达截面 (RCS)。
进一步了解 WaveFarer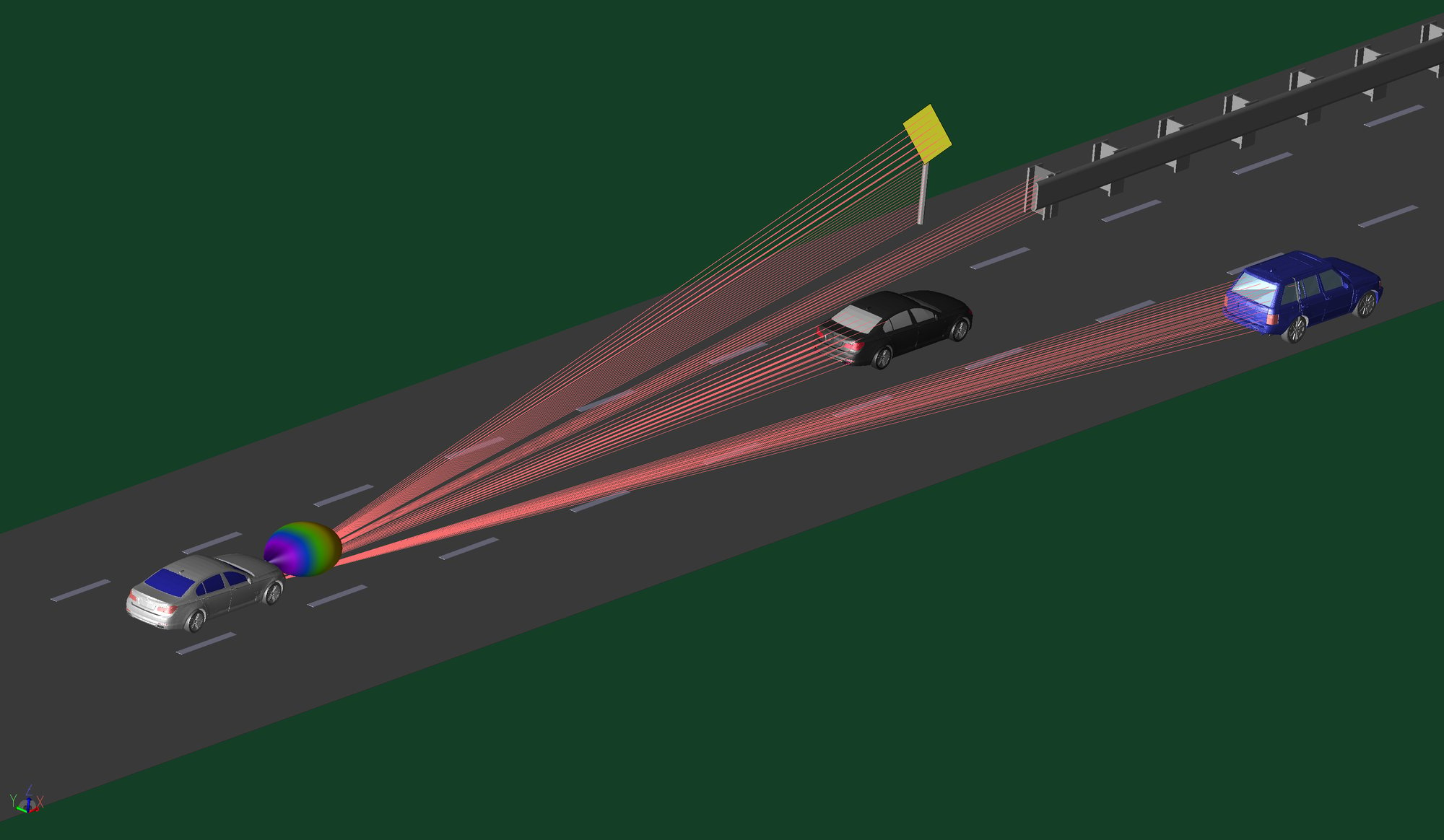
-
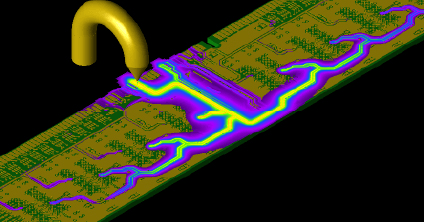
XGtd® 用于大型电气平台的远区辐射、RCS 和 EMI/EMC
XGtd 是一种基于射线的电磁分析工具,用于评估车辆或船只对天线辐射的影响、预测天线之间的耦合以及预测雷达截面(RCS)。 它非常适合频率较高或平台非常大的应用,在这些应用中,全物理方法的要求可能会超出可用的计算资源。
进一步了解 XGtd

愉快的业务协作--这与您选择的软件同样重要。
Remcom 的与众不同之处
以客户为中心
Remcom 致力于倾听客户的心声,了解他们的需求,每次发布新版本时,都会将客户要求的功能直接添加到软件中。自电磁场仿真软件问世以来,我们一直在提供电磁专业技术和解决方案,因此您可以相信,我们在产品设计和功能以及支持方式方面积累了多年的经验。
一些信任我们的客户